Amit Kumar : Life Is Learning!

17 Jun 2015

GSoC : This week in SymPy #3

Open Source · GSoC · SymPy

Hi there! It’s been three weeks into GSoC, & I have managed to get some pace. This week, I worked on creating ComplexPlane Class.

  Progress of Week 3

The major portion of this week went onto creating ComplexPlane Class. PR #9438

Design

The design for the ComplexPlane class supports both forms of representation of Complex regions in Complex Plane.

  • Polar form

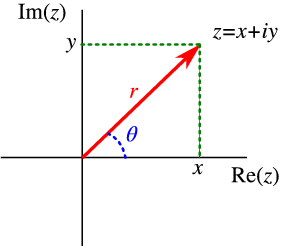
Polar form is where a complex number is denoted by the length (r) (otherwise known as the magnitude, absolute value, or modulus) and the angle (θ) of its vector.

  • Rectangular form

Rectangular form, on the other hand, is where a complex number is denoted by its respective horizontal (x) and vertical (y) components.

Initial Approach

While writing code for ComplexPlane class, we started with the following design: Input Interval of a and b interval, as following:

ComplexPlane(a_interval, b_interval, polar=True)

Where a_interval & b_interval are the respective intervals of x and y for complex number in rectangular form or the respective intervals of r and θ for complex number in polar form when polar flag is True.

But the problem with this approach is that we can’t represent two different regions in a single ComplexPlane call, i.e. , for example let say we have two rectangular regions be represented as follows:

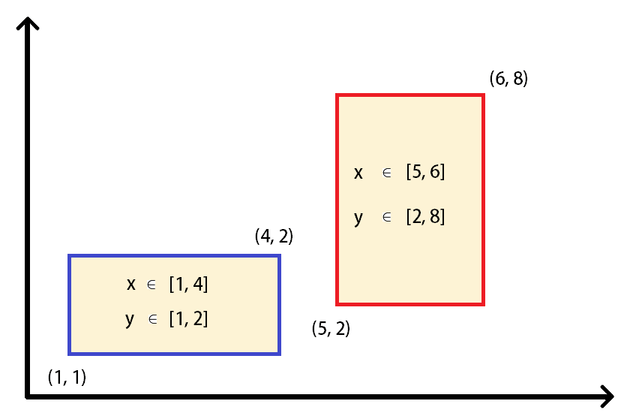
We have to represent this with two ComplexPlane calls:

rect1 = ComplexPlane(Interval(1, 4), Interval(1, 2))
rect2 = ComplexPlane(Interval(5, 6), Interval(2, 8))
shaded_region = Union(rect1, rect2)

Similiary for, the following polar region:

halfdisk1 = ComplexPlane(Interval(0, 2), Interval(0, pi), polar=True)
halfdisk2 = ComplexPlane(Interval(0, 1), Interval(1, 2*pi),
                         polar=True)
shaded_region = Union(halfdisk1, halfdisk2)

Better Approach

The solution to the above problem is to wrap up two calls of ComplexPlane into one. To do this, a better input API was needed, and the problem was solved with the help of ProductSet.

Now we take input in the form of ProductSet or Union of ProductSets:

The region above is represented as follows:

  • For Rectangular Form
psets = Union(Interval(1, 4)*Interval(1, 2),
              Interval(5, 6)*Interval(2, 8))
shaded_region = ComplexPlane(psets)
  • For Polar Form
psets = Union(Interval(0, 2)*Interval(0, pi),
              Interval(0, 1)*Interval(1, 2*pi))
shaded_region = ComplexPlane(psets, polar=True)

Note: The input θ interval for polar form tolerates any interval in terms of π , it is handled by the function normalize_theta_set (wrote using _pi_coeff function), It normalizes θ set to an equivalent interval in [0, 2π), which simplifies various other methods such as _union, _intersect.

from __future__ import plan Week #4:

This week I plan to polish my pending PR’s to get them Merged & start working on LambertW solver in solveset.

$ git log

That’s all for now, looking forward for week #4. :grinning:

Related Posts