Spoj FCTRL2 Explanation and Solution

Problem:

In this Problem , we are required to find Factorials of numbers ranging from 1 to 100, but Since an unsigned 64-bit Integer can store upto 19 decimal digits, where as 100! has 150+ digits, so we can’t use Int Data type.

The simplest data structure which can be used to store such results is an Array. In the simplest form we can store 1-digit at every index of array.

How to store a two (or more) digit number in an Array (one digit per index) ?

We need to store the input ‘n’ (1-100) into an array to find it’s Factorial To store a Number in an array, we can grab the digits from least significant position (For Example 1456) one by one and put it into the array. For example: To put 123 into an array (let say a[50]), we will grab the last digits one by one, final array would be given as a[] = {3,2,1} i.e. a[0]=3, a[1]=2, a[2]=1 & so on…

LOGIC used for this: Let n = 123 then 1). let rem = n%10 (this means remainder when n is divided by 10) 2. a[index] = rem 3. n = n/10 (this removes the last digit from n, Now we are ready to grab the second last digit & so on) Repeating this step iteratively, we can save n into an array. — How To Find the Factorial of the Number stored in array?

After we have put the input number (1-100) into an array, we have to now find its Factorial. To do that we have to multiply the number ‘n’ with (n-1), (n-2) … & so on …3.2.1 . Now we need to find an Algorithm for multiplying an Integer with a number stored into an array & we can use that algorithm for all multiplications.

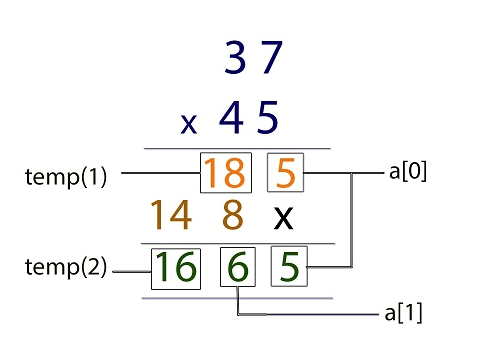
Let us take an Example: Let the n be 45, so we have to find it’s factorial
45! = 45 x 44 x 43 x … x 37 x … 4 x 3 x 2 x 1. Now put the number 45 into a sufficiently large array (such as a[200]). Now lets us multiply the array a[] = {5,4} with a number, let say 37

The array will be: a[0] = 5 a[1] = 4 and the value of m will be 2 specifying that there are 2 digits in the array currently.

Codechef Tutorial

Now, to multiply this array with the value 37. We start off from the index 0 of the array to index 1. At every iteration, we calculate 37 * a[index]. We also maintain a temporary variable called temp which is initialized to 0. Now, at every step, we calculate x = a[index] * 37 + temp. The new value of a[index] will be x % 10 and the new value of temp will be temp / 10. We are simply carrying out multiplication the way it is carried out usually (The Process is shown in Figure below). So, for the current situation, the iterations will be something like this.

Initialize temp = 0 Iteration 1 : array = (5, 4) temp = 0 index = 0, a[index] = 5 x = a[index] * 37 + temp = 5 * 37 + 0 = 185. the new value of a[index] = 185 % 10 which is 5 and the new value of temp is 185 / 10 which is 18

Iteration 2 : array : (5, 4) temp = 18 index = 1, a[index] = 4 x = a[index] * 37 + temp = 4 * 37 + 18 = 166. the new value of a[index] = 166 % 10 which is 6 and the new value of temp is 166 / 10 which is 16

We have finished 2 iterations and this is the value of ‘m‘, the array size at the moment. The required number of iterations is now over, but the value oftemp is still greater than 0. This means that the current value of temp is to be incorporated into the array. For that, we keep appending the last digit oftemp to the array and divide temp by 10 till temp becomes 0. So, we will get something like Iteration 1 : temp = 16 , array = (5, 6) So, we add 16 % 10 to the array so that the array becomes (5, 6, 6) and we divide temp by 10 so that temp becomes 1. We update the value of ‘m’ to m + 1 that is m = 3 Iteration 2 : temp = 1, array = (5, 6, 6) Now, we add 1 % 10 to the array so the array becomes (5, 6, 6, 1) and we divide temp by 10 so that temp becomes 0. We update the value of ‘m’ to m + 1 that is m = 4

The value of temp is now 0 and our multiplication is now over. The final array we get is (5, 6, 6, 1)

Voila, we have the answer to 45 * 37 in our array with the Least significant digit in the 0th position. :)

For finding the factorial, we need to carry out this exact multiplication operation at every step as we loop from 1 to N. At the end of the Nth iteration, our array will contain the answer and the value of m will be the number of digits in the answer. We can then just print the array from the Most significant digit to the least for the answer.

Code in C++

// Source Code Of Above Algorithm:
#include<iostream>
using namespace std;
int main() {
int t;
    cin>>t;
    while(t--) {
        int a[200],rem,i=0,n,m=0,flag;
        cin>>n;
        flag = n; 
 
        while(flag!=0)  {
            rem = flag%10;
            a[i] = rem;
            flag = flag/10;
            i++;  
             m++;
        } 
 
         int temp,x=0,index=0;
         for(i=2;i<n;i++)  {
             temp = 0;
             for(index=0;index<m;index++) {
                 x = a[index]*i + temp;
                 a[index] = x%10;
                 temp = x/10;
              }
  
              while(temp!=0) {
                  a[index] = temp % 10;
                  temp = temp/10;
                  index++;
                  m++;
               }
            }
 
            for(i=m-1;i>=0;i--) {cout<<a[i];}
                cout<<"\n";
            }
    return 0;
}

Thanks to this Tutorial at Codechef

Code in Python

For Python Freaks, it’s a cakewalk. 10 lines of code!

def fact(a):
    factl = 1
    for i in range(1,a+1,1):  factl = factl*i
    return factl
def main():
    t = int(input())
    for i in range(t):
        n = int(input())
        print(fact(n))
if __name__ == "__main__":main()